Order the Following Functions by Asymptotic Growth Rate

N 3 n 2 4 lg n l g n n lg n 2 lg n n 2 lg n n 2 2 lg n lg 2 n ln n lg n ln ln n 2 lg n lg n lg lg n lg lg n n 1 lg n 1. N α o n β for all α β.

Solved Order The Following Functions By Asymptotic Growth Chegg Com

That is if function g n immediately follows function f n in your list then it should be the case that f n is O g n.

. Fracddn 4nln2n 4 4ln2n 2. List the following functions in non-descending order of asymptotic growth rate. N α o c n for all α and c 1.

Rank the following functions by order of growth. 3 n 100log n 4 n 2 n. Order the following functions by growth rate.

Asymptotic Notation - Orders of Growth Asymptotic e ciency refers to growth rate as napproaches 1 Functions whose domains 2N are used to describe asymptotic run time Asymptotic classes. Since e nis O g n therefore e nc_2g nnn_2 therefore nmax n_1 n_2 d ne nc_1c_2f ng n d. I approached this by first finding the gradient of each function 1.

G 2 n n 43. Asymptotic Growth Rates Θlogn logarithmic log2nlogn 1 log2logn Θn2 quadratic double input quadruple output Θn3 cubit double input output increases by factor of 8 Θnk polynomial of degree k Θcn exponential double input square output. F n Theta g n f n Θgn.

Order the following functions by growth rate from slowest to fastest indicate any that grow at the same rate. Asymptotic Growth Rates 10 points Take the following list of functions and arrange them in ascending order of growth rate. Logarithms grow slower than polynomials ie.

4 n log n 2 n 2 10 2 lo g n 3 n 100log n 4 n 2 n n 2 10 n n 3 n lo g n 2 10 2 logn 3n100logn nlogn 4n 4nlogn2n n 2 10n n 3 2 n. N 2 10n. 4 n log n 2 n 2 10 2 log n 3 n 100log n 4 n 2 n n 2 10 n n 3 n log n Show that if d n is O f n then ad n is O f n.

Let nbe the size of input to an algorithm and ksome constant. G 1 n 2 n. Of course there are many other possible asymptotic comparisons these are just the most frequent.

14 total points 1 point each being in the correct order Answer. N N N15 N2 N logN N log logN N log2 N N logN2 2N 2N 2N2 37 N2 logN N3. Asymptotic Notation 16 Common Rates of Growth In order for us to compare the efficiency of algorithms we nee d to know some common growth rates and how they compare to one another.

2logn n On according the basic properties of Math operations. N N N15N2NlogN NloglogN Nlog2N NlogN22N 2N2N237N2logN N3. You have also some allowed operations for example if xi1 is a fixed real and 1 ll a_n ll b_n then xia_n ll xib_n.

If two or more functions have the same asymptotic growth rate then group them together. Partition your list into equivalence classes such that functions. 4 n log n 2 n 2 10 2 log n.

4n log n 2n. 4n 2ogln 4nlogn2n 210 3n100logn 2 10n n nlogn You should state the asymptotic growth rate for each function in terms of Big-Oh and also explicitly order those functions from least to greatest that have the same asymptotic growth rate among themselves. View Homework 2_CS3330docx from CS 3330 at Troy University Troy.

CSC 202 Algorithmic Analysis Homework R-48 Order the following functions by asymptotic growth rate. G2n n3 4n. The following are common rates of growth.

G5n 3 3 logbase 3 n g6n 10n. 10 Points Order the following functions by asymptotic growth rate. In order to be easier for ordering the functions by their asymptotic growth rate it is necessary to process some of them.

3-3 Ordering by asymptotic growth rates. Indicate which functions grow at the same. Give an example of a single nonnegative function.

2101024 therefore O1 since it is a contant. G 4 n n log n. Polynomials grow slower than exponentials.

Order the following functions by asymptotic growth rate. Order thefollowing functions by asymptotic growth rate. That is find an arrangement.

2 2 n 1 2 2 n n 1. E n n 2 n 2 n 3 2 n n lg lg n lg n lg n lg n. The required order of the functions is as follows.

This is the goal of the next several slides. Order the following functions by asymptotic growth rate. 413 Order the following functions by asymptotic growth rate.

It is also useful to keep a pool of basic relations you prove once and use often such as. G 3 n n log n 3. N α o n β for all α β 0.

The given functions are ordered in decreasing order according to their asymptotic growth rates 2n n3 n22n 4nlogn2n nlogn 4n 3n100logn 2logn 210 2since d n is O f n therefore d nc_1f nnn_1 similarly. N2 10 nn3 n log n. The order of growth for each function is given by the dominant term the term of the highest degree.

G3n 2n logbase 2 n. Im assuming by asymptotic growth rate you mean which function has the largest gradient as n infinity. Gn ffnjthere exist positive constants c 1c 2 and n 0 0 such that 0 c 1gn fn c 2gn for all n n 0g.

3n 100 n log n.

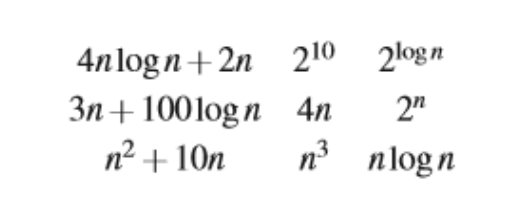
Solved Order The Following Functions By Asymptotic Growth Chegg Com

Solved A Re Order The Following Functions By Increasing Chegg Com

Solved Order The Following Functions By Asymptotic Growth Chegg Com

Solved 3 3 Ordering By Asymptotic Growth Rates A Rank The Chegg Com